TRAPEZOIDES
En los trapezoides podemos encontrar:
Trapezoide cruzado
Se compone de dos triángulos cuyos interiores son disjuntos. la unión de dichos interiores es el interior del cuadrilátero. Un cuadrilátero cóncavo tiene un ángulo 'entrante' cuya medida cumple . El cuadrilátero cruzado determina una partición del plano en tres clases disyuntas: el interior, el exterior y el mismo cuadrilátero.
Tiene dos diagonales disyuntas que están en el exterior AC y BD, excepto sus extremos. La suma de sus ángulos interiores no alcanza 360º. Los lados AD y BC prolongados sitúan el paralelogramo en dos semiplanos opuestos.
Trapezoide cóncavo
Si consideramos el punto C vértice del ángulo entrante, el segmento AC determina dos triángulos ABC y ACD, cuyos interiores unidos con el segmento AC forman el interior del cuadrilátero. La suma de los ángulos de un cuadrilátero cóncavo es 360º.
Tiene dos diagonales disyuntas la AC en el interior, la BD en el exterior, excepto los extremo.Los lados BC y CD con sus prolongaciones sitúan el cuadrilátero en dos semiplanos opuestos.
Trapezoide convexo
se ubica en un solo semiplano respecto de cualquier lado y de su prolongación. Un punto está en el interior del trapezoide si se ubica entre los cortes que determina una recta, que contiene dicho punto, con dos lados del trapezoide. Tiene dos diagonales mutuamente secantes que están en el interior de la figura. Sus ángulos suman exactamente 360º.
Se clasifican en trapezoides simétricos, cuyos ángulos opuestos son iguales; y, asimétricos si tal caso no ocurre. Los trapezoides simétricos se llaman también antiparalelogramo, trapezoide biisósceles, deltoide.
 . El cuadrilátero cruzado determina una partición del plano en tres clases disyuntas: el interior, el exterior y el mismo cuadrilátero.
. El cuadrilátero cruzado determina una partición del plano en tres clases disyuntas: el interior, el exterior y el mismo cuadrilátero.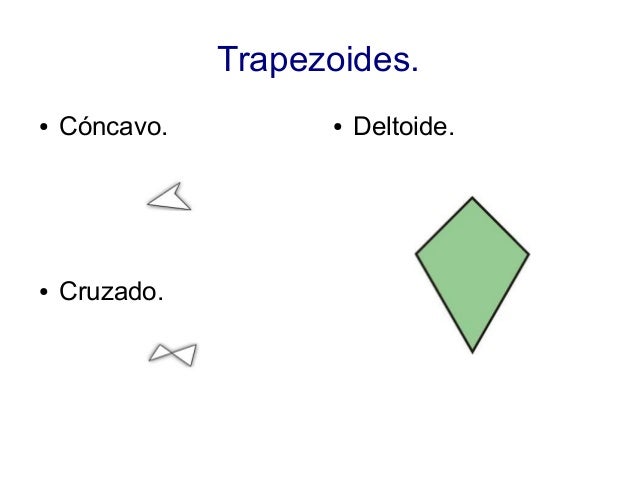
No hay comentarios:
Publicar un comentario